Jrgeometry: 12 books

What is the center of a triangle? Do you need a straight forward method for finding the orthocenter of a triangle? Do you need to see how the Law of Sines is developed? Do you need to see how the geometric mean is applied to triangles? Do you need to better understand triangle similarity? Do you need...

The definition of a proof, the general structure of a proof, direct and indirect proofs, illustrations. 24 geometry proofs.

How can lengths be used to find area or volume? How can length and area be used to find volume? How can area be used to find length? How can volume be used to find area or length? What are hidden shapes, and how can they be used to find indirect measurements? This study guide shows how to make indirect...

How are area and surface area formulas for circles, spheres, oblique and right circular cones, sectors, segments, and other Eucildean shapes developed? Need help finding the area or surface area? The Area Study Guide can help you. 53 solved problems.

The inside and outside of a hypersphere is geometrically described. When diameters move into geometric four-dimensional space, how is a hypersphere formed? Can dimensional cross-sections of a hypersphere be realized? How can the rotation of a hypersphere be described? What is the boundary of a hypersphere?...

What is distance? What is a geodesic? What are functions on the surface of a sphere or globe? What is a geodesic midpoint? Do you need more insight on spherical triangles? This study guide can help answer these questions. 17 solved problems.

Why is the interior angle sum of an n-sided polygon equal to (n-2)180 deg? Why is the exterior angel sum of a polygon 360 deg? Need help with understanding what a rhombus or a kite is? Need insight on the midsegment of a trapezoid? This study guide provides this information and has 22 solved polygon problems.

How can the circle formulas be realized? How are line segments and angles related to circles? What is an arc measure as compared to an arc length? The Circles study guide can help you. 26 solved problems.

How are the Euclidean volume formulas developed? How are the formulas applied for problem solving? Need help finding volumes of Euclidean oblique shapes? The Volume study guide can help you. 15 solved problems.

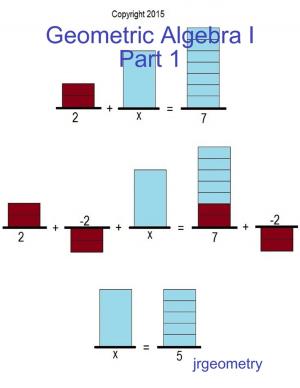
Using simple geometric shapes, a closer look will be taken of the following: A) the number Line, B) operations with integers C) long division, D) fractions, E) solving the following: linear equations, linear inequalities, absolute value linear equations, absolute value linear inequalities. Solving Linear...

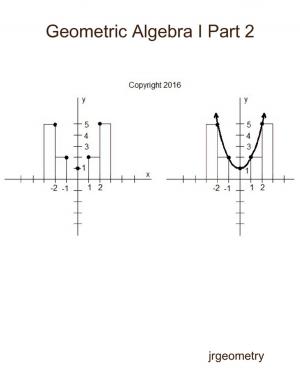
Need help with equations and inequalities of lines, two-variable linear absolute value, parabolas, and cubics? By using simple geometric shapes, this studyguide will help. 48 pages, 49 solved problems, all well-illustrated solutions.

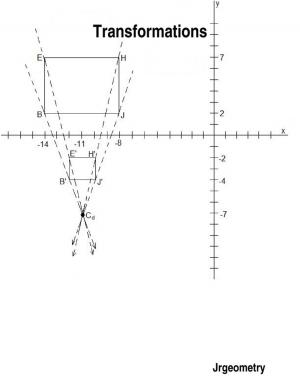
How can a Euclidean shape change and remain the same type of shape? What are the different ways that a Euclidean shape can change and still remain the same type of shape? How can a Euclidean shape change and remain either congruent or noncongruent? How can these changes be used to generate patterns...